Le chiffrement de Vigenère

Le chiffrement de Vigenère ressemble beaucoup au chiffrement de César, à la différence près qu'il utilise une clef plus longue afin de pallier le principal problème du chiffrement de César: le fait qu'une lettre puisse être codée d'une seule façon. Pour cela on utilise un mot clef au lieu d'un simple caractère.
On associe dans un premier temps à chaque lettre un chiffre correspondant.

A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26

Il consiste à coder un texte avec un mot en ajoutant à chacune de ses lettres la lettre d'un autre mot appelé clé. La clé est ajoutée indéfiniment en vis-à-vis avec le texte à chiffrer, puis le code ASCII de chacune des lettres de la clé est ajouté au texte à crypter. Par exemple le texte "rendezvousamidi" avec la clé bonjour sera codé de la manière suivante:

Texte original:

r	e	n	d	e	z	v	o	u	s	a	m	i	d	i
18	5	14	4	5	26	22	15	21	19	1	13	10	4	10

Clé:

b	o	n	j	o	u	r
2	15	14	10	15	21	18

Texte crypté

r+b

e+o

n+n

d+j

e+o

z+u

v+r

o+b

u+o

s+n

a+j

m+o

i+u

d+r

i+b

18+2

5+15

14+14

4+10

5+15

26+21

22+18

15+2

21+15

19+14

1+10

13+15

10+21

4+18

10+2

Pour déchiffrer ce message il suffit d'avoir la clé secrète et faire le déchiffrement inverse, à l'aide d'une soustraction.

Bien que ce chiffrement soit beaucoup plus sûr que le chiffrement de César, il peut encore être facilement cassé. En effet, lorsque les messages sont beaucoup plus longs que la clef, il est possible de repérer la longueur de la clef et d'utiliser pour chaque séquence de la longueur de la clef la méthode consistant à calculer la fréquence d'apparition des lettres, permettant de déterminer un à un les caractères de la clef...

Pour éviter ce problème, une solution consiste à utiliser une clef dont la taille est proche de celle du texte afin de rendre impossible une étude statistique du texte crypté. Ce type de système de chiffrement est appelé système à clé jetable. Le problème de ce type de méthode est la longueur de la clé de cryptage (plus le texte à crypter est long, plus la clef doit être volumineuse), qui empêche sa mémorisation et implique une probabilité d'erreur dans la clé beaucoup plus grande (une seule erreur rend le texte indéchiffrable...).

DES, le cryptage à clé secrète

Au début des années 70, la NBS (National Bureau of Standards) a lancé un appel dans le Federal Register pour la création d'un algorithme de cryptage répondant aux critères suivants:

• ayant un haut niveau de sécurité lié à une clé
• compréhensible
• ne devant pas dépendre de la confidentialité de l'algorithme
• adaptable et économique
• efficace et exportable

C'est un système de chiffrement par blocs de 64 bits, dont le dernier octet (8 bits) sert de test de parité (pour vérifier l'intègrité des données). Il consiste à faire des combinaisons, des substitutions et des permutations entre le texte à chiffrer et la clé, en faisant en sorte que les opérations puissent se faire dans les deux sens (pour le décryptage). La clé est codée sur 16 bits et formée de 16 blocs de 4 bits, généralement notés k₀ à k₁₅. Etant donné que 8 bits de la clé sont réservés pour le test de la parité, "seulement" 56 bits servent réellement à chiffrer, ce qui représente tout de même 2⁵⁶ possibilités, c'est-à-dire 72*10¹⁵ clés possibles...
Les grandes lignes de l'algorithme sont les suivantes:

• fractionnement du texte en blocs de 64 bits
• permutation des blocs
• découpage des blocs en deux parties: gauche et droite
• Etapes de permutation et de substitution répétées 16 fois (appelées rondes)
• recollement des parties gauche et droites puis permutation initiale inverse

Algorithme du DES:

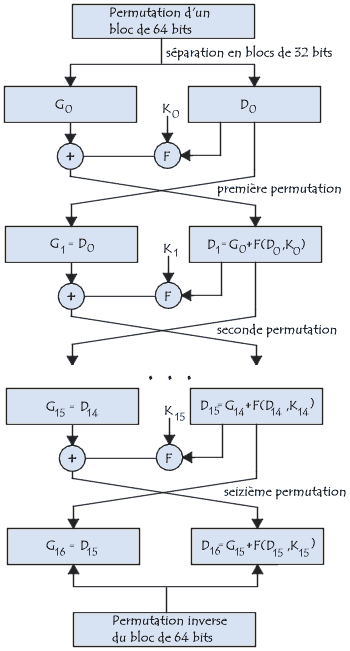
Problèmes de la méthode

En 1990 Eli Biham et Adi Shamir ont mis au point la cryptanalyse différentielle qui recherche des paires de texte en clair et des paires de texte chiffrées (cette méthode marche jusqu'à un nombre de rondes inférieur à 15 d'où un nombre de 16 rondes dans l'algorithme présenté ci-dessus).

D'autre part, même si une clé de 56 bits donne un nombre énorme de possibilités, de processeurs permettent de calculer plus de 10⁶ clés par seconde, ainsi, utilisés parallèlement sur un très grand nombre de machines, il peut être possible à un grand organisme (un Etat par exemple) de trouver la bonne clé...